Forecasting Tutorial#

In this tutorial, we will show how to use Karman to forecast thermospheric density. In particular, a pre-trained time fusion transformer will be used for this.

Imports#

import sys
sys.path.append('../../')
import karman
import pandas as pd
import torch
import numpy as np
import random
from torch.utils.data import RandomSampler, SequentialSampler
import pickle as pk
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import math
from sklearn.preprocessing import QuantileTransformer

torch.set_default_dtype(torch.float32)

Let’s now define a few hyperparameters

#here we set a few things, like the lag in minutes and the resolution of the data
lag_minutes=10000
resolution_minutes=100
features_to_exclude_thermo=["all__dates_datetime__", "tudelft_thermo__satellite__", "tudelft_thermo__ground_truth_thermospheric_density__[kg/m**3]", "all__year__[y]", "NRLMSISE00__thermospheric_density__[kg/m**3]"]
features_to_exclude_thermo+='celestrack__ap_average__,JB08__d_st_dt__[K],space_environment_technologies__f107_obs__,space_environment_technologies__f107_average__,space_environment_technologies__s107_obs__,space_environment_technologies__s107_average__,space_environment_technologies__m107_obs__,space_environment_technologies__m107_average__,space_environment_technologies__y107_obs__,space_environment_technologies__y107_average__'.split(',')

data_path={"omni_indices":'../../data/omniweb_data/merged_omni_indices.csv', 
           "omni_solar_wind":'../../data/omniweb_data/merged_omni_solar_wind.csv', 
           "omni_magnetic_field":'../../data/omniweb_data/merged_omni_magnetic_field.csv',
           "soho":'../../data/soho_data/soho_data.csv',
           "msise":'../../data/nrlmsise00_data/nrlmsise00_time_series.csv'}

Data Preparation#

We load (if already prepared) or prepare the time series data:

resolution_minutes=100
try:
    with open("ts_data_normalized.pk", "rb") as f:
        ts_data_normalized = pk.load(f)
except:
    print("Creating time series data normalized, note that this can take a couple of minutes. We recommend to store it as a pickle file for next times to spare this time.")
    ts_data_normalized = karman.util.normalize_time_series_data(resolution=resolution_minutes,
                                                                 data_path=data_path)
    #with open("ts_data_normalized.pk", "wb") as f:
    #    pk.dump(ts_data_normalized, f)

#let's pickle it:
#with open("ts_data_normalized.pk", "wb") as f:
#    pk.dump(ts_data_normalized, f)
#let's load from pickle to make things faster:
#with open("ts_data_normalized.pk", "rb") as f:
#    ts_data_normalized = pk.load(f)

Now the lat/lon grid:

import numpy as np
# We build the model entries:
n_grid=50
u, v = np.linspace(0, 1, n_grid), np.linspace(0, 1, n_grid)
longitude, latitude = np.sort(2 * np.pi * u), np.sort(np.arccos(2 * v - 1) - np.pi / 2)
lonlat_grid = np.stack([*np.meshgrid(longitude, latitude, indexing="ij")], axis=2).reshape(-1, 2) 
lonlat_grid[:,0]-=np.pi

and the altitude and dates:

#let's prepare the inputs to the model and run it:
longitudes=list(np.rad2deg(lonlat_grid[:,0],dtype=np.float32))
latitudes=list(np.rad2deg(lonlat_grid[:,1],dtype=np.float32))
n_samples=len(longitudes)
altitudes=[300000.]*n_samples#250km in meters
dates=['2024-05-31 23:00:00']*n_samples

Time Fusion Transformer Forecasting Model#

forecasting_model=karman.density_models.ForecastingModel(state_size=32,attention_heads=5)

let’s load a pre-trained one:

model_path_ts='../../models/ts_karman_model_tft_ss32_heads5_lag10000_resolution100_valid_mape_15.906_params_289457.torch'
forecasting_model.load_model(model_path=model_path_ts,device='cpu')

number of parameters: 289457
Loaded model with 289457 parameters

/home/ga00693/karman/karman/density_models.py:145: FutureWarning: You are using `torch.load` with `weights_only=False` (the current default value), which uses the default pickle module implicitly. It is possible to construct malicious pickle data which will execute arbitrary code during unpickling (See https://github.com/pytorch/pytorch/blob/main/SECURITY.md#untrusted-models for more details). In a future release, the default value for `weights_only` will be flipped to `True`. This limits the functions that could be executed during unpickling. Arbitrary objects will no longer be allowed to be loaded via this mode unless they are explicitly allowlisted by the user via `torch.serialization.add_safe_globals`. We recommend you start setting `weights_only=True` for any use case where you don't have full control of the loaded file. Please open an issue on GitHub for any issues related to this experimental feature.
  ts_karman_model.load_state_dict(torch.load(model_path,map_location=torch.device(device)))

density_nn=forecasting_model(dates=dates, 
                             altitudes=altitudes,
                             longitudes=longitudes,
                             latitudes=latitudes,
                             device=torch.device('cpu'),
                             ts_data_normalized=ts_data_normalized,
                             )

NRLMSISE-00 Data#

We also run NRLMSISE-00, for comparison. Keep in mind that the ML models are not trained with this, but directly with precise-orbit determination-derived satellites data.

Note that while the NRLMSISE-00 data is generated as usual, the TFT model is actually forecasting, so it uses data up to 100 minutes before the event and forecasts based on that.

#let's extract the SW inputs to compute NRLMSISE-00:
sw_df=karman.util.find_sw_from_thermo(pd.to_datetime(dates),karman.density_models.df_sw)
ap=sw_df['celestrack__ap_average__'].values
f107=sw_df['space_environment_technologies__f107_obs__'].values
f107A=sw_df['space_environment_technologies__f107_average__'].values

from nrlmsise00 import msise_flat
d=pd.to_datetime(dates)
density_nrlmsise00=msise_flat(d.to_pydatetime(), np.array(altitudes)*1e-3, latitudes, longitudes, f107A, f107, ap)[:,5]*1e3

Visualization#

# we setup the longitude x latitude grid, and compute the relative error (in %)
lon_grid = np.rad2deg(lonlat_grid[:, 0].reshape((n_grid, n_grid)))
lat_grid = np.rad2deg(lonlat_grid[:, 1].reshape((n_grid, n_grid)))

# we now create a figure with a globe projection on top:
fig, ax = plt.subplots(
    figsize=(18, 12),
    nrows=1,
    ncols=2,
    subplot_kw={"projection": ccrs.Mollweide(central_longitude=0)},
)
# we flatten the axis and remove the last figure
ax = ax.ravel()
ax[-1].axis("off")

# we plot NRLMSISE-00 on the first figure:
ax[0].pcolormesh(
    lon_grid,
    lat_grid,
    density_nrlmsise00.reshape((n_grid, n_grid)),
    transform=ccrs.PlateCarree(),
    vmin=min(density_nrlmsise00),
    vmax=max(density_nrlmsise00),
)
ax[0].set_global()
ax[0].coastlines()
# ax[0].gridlines()
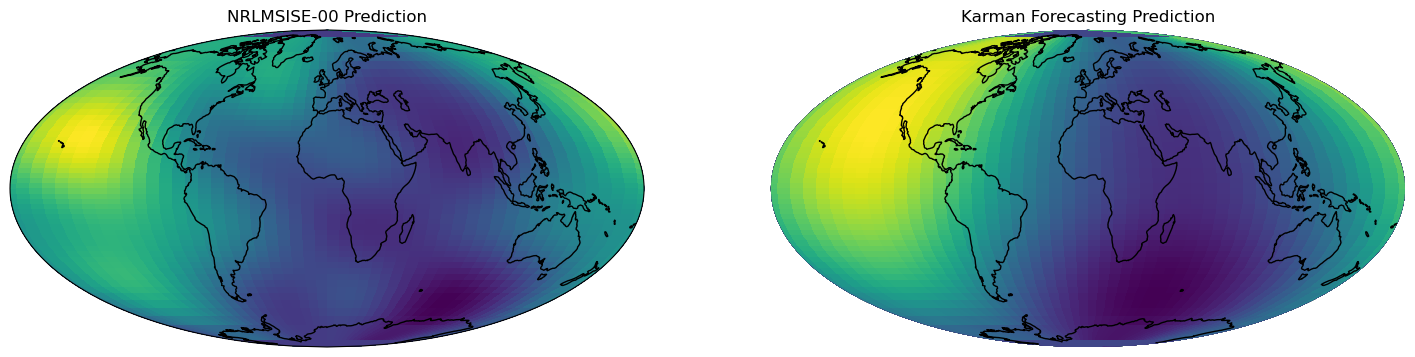
ax[0].set_title("NRLMSISE-00 Prediction")

# the NN prediction on the second:
im2 = ax[1].pcolormesh(
    lon_grid,
    lat_grid,
    density_nn.reshape((n_grid, n_grid)),
    transform=ccrs.PlateCarree(),
    vmin=min(density_nn),
    vmax=max(density_nn),
)
ax[1].set_global()
ax[1].coastlines()
# ax[1].gridlines()
ax[1].set_title("Karman Forecasting Prediction")
plt.show()

../_images/d35f445ba31fdb2180822bc996400b16bd6a0c9352c188c4ccd36da038e61ac7.png

Forecasting Tutorial

Contents